7031. Существенные инверсии

Рассмотрим произвольную последовательность чисел x₁, x₂, ..., x_n. Пару индексов (j, k) называют инверсией (нарушением порядка), если j < k и x_j > x_k. Для произвольного неотрицательного числа t пару индексов (j, k) назовем t-существенной инверсией, если j < k и x_j > x_k + t.

Подсчитайте количество t-существенных инверсий в последовательности x₁, x₂, ..., x_n.

Вход. Первая строка содержит два целых числа n (1 ≤ n ≤ 50000) и t (0 ≤ t ≤ 10⁹). Во второй строке записаны целые числа x₁, x₂, ..., x_n, по модулю не превосходящие 10⁹.

Выход. Вывести количество t-существенных инверсий в последовательности x₁, x₂, ..., x_n.

Пример входа	Пример выхода
5 2 1 2 7 3 6	1

РЕШЕНИЕ

сортировка слиянием

Анализ алгоритма

Реализуем классическую сортировку слиянием. При подсчете 0-инверсий (обычных) их количество увеличивалось на n – i + 1 когда a_i > b_j и элемент b_j переносился в сливаемый массив.

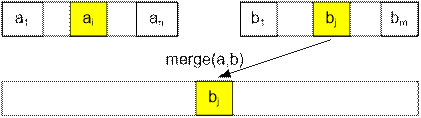
В случае t-существенных инверсий при переносе b_j в результирующий массив их количество следует увеличить на число, равное количеству таких a_k, что a_k > b_j + t. Пусть q – наименьший индекс левого массива, для которого a_q > b_j + t. Тогда все элементы a_q, a_q+1, …, a_n с элементом b_j будут образовывать t-существенные инверсии, то есть число искомых инверсий при переносе b_j в результирующий массив следует увеличить на n – q + 1.

Пример

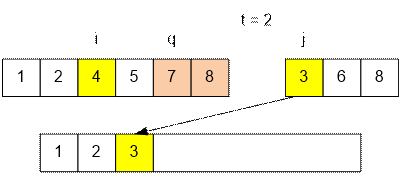
Рассмотрим слияние двух массивов при t = 2. Пусть текущие индексы i и j указывают на числа 4 и 3, число 3 переносится в результирующий массив. Наименьшим числом из левого массива, большего 3 + t, будет 7 – на него будет указывать индекс q. Таким образом число 3 образует две существенные 2-инверсии с числами 7 и 8.

Реализация алгоритма

Входную последовательность будем хранить в массиве m.

#define MAX 50001

int m[MAX];

Слияние отсортированных массивов a[bleft] ... a[bright] и a[cleft] ... a[cright] в a[bleft] ... a[cright]. Отметим, что у нас всегда bright + 1 = cleft. Для слияния используем дополнительный массив res. Сначала скопируем a[bleft ... bright] в res[0 … len – 1], где len = bright – bleft + 1, после чего сольем res[0 … len – 1] и a[cleft ... cright] в a[bleft ... cright].

void merge(int *a, int bleft, int bright, int cleft, int cright)

{

int i, len = bright - bleft + 1, resCur = 0, q = 0;

int *res = new int[len];

memcpy(res,a + bleft,len*sizeof(int));

while((resCur < len) && (cleft <= cright))

{

while((res[q] <= a[cleft] + t) && (q < len)) q++;

if (res[resCur] <= a[cleft]) a[bleft++] = res[resCur++];

else a[bleft++] = a[cleft++], swaps += len - q;

}

while (resCur < len) a[bleft++] = res[resCur++];

delete[] res;

}

Сортируем массив a[left ... right] методом “разделяй и властвуй”. Для этого разделим его на две части a[left ... middle] и a[middle + 1 ... right], отсортируем отдельно каждую из них, после чего произведем слияние.

void mergeSort(int *a, int left, int right)

{

if (left >= right) return;

int middle = (left + right) / 2;

mergeSort(a,left,middle);

mergeSort(a,middle+1,right);

merge(a, left, middle, middle + 1, right);

}

Основная часть программы. Считываем входной массив, запускаем сортировку слиянием, в которой подсчитываем количество t-существенных инверсий swaps.

scanf("%d %d",&n,&t);

for(swaps = i = 0; i < n; i++) scanf("%d",&m[i]);

mergeSort(m, 0, n - 1);

printf("%d\n",swaps);